Neural-network approximation of magnetic interactions
check out chapter 6 of my PhD thesis for more details of this work.
Introduction
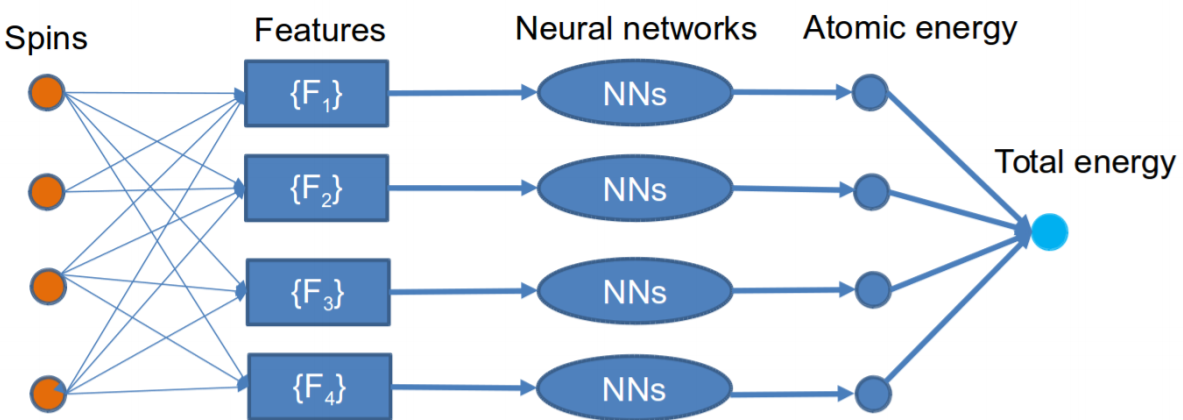
Artificial intelligence (AI) has been referred to as the “fourth industrial revolution”. As the core of AI, the application of machine learning has gone beyond industry. It drives a new way for researchers to extract physical laws or knowledge from experiments or simulations. In computational materials science, a well-known problem is to construct the structure-energy relationship, i.e., calculate the potential energy for a given atomic or magnetic configuration. Machine-learning is playing an increasing role in this problem as the trained machine-learning models can save orders of magnitudes in the computational cost of electronic-structure models (ESM) such as DFT, tight-binding, or bond-order potentials, and make it possible to perform large-scale simulations. For non-magnetic materials, there have already been many machine-learning models available, e.g., Gaussian approximation potentials, neural-network potentials, and moment tensor potentials. However, for magnetic materials, the machine-learning models are still in infancy. As a first step to develop machine-learning approaches for magnetic materials, we propose in this work a neural-network potential for magnetic systems with a homogeneous atomic environment. Furthermore, we employ a perturbation approach to correct errors of thermodynamic calculations with the machine-learning model.
